- Plataformas
- Programação comercial
- Assessores para NetTradeX
- Criação de uma rede neural em NTL +
Criação de uma rede neural em NTL +
Introdução
As redes neurais artificiais - são modelos matemáticos e as suas implementações de software ou hardware são construídos sobre o princípio da organização e funcionamento das redes neurais biológicas - redes de células nervosas (neurônios) do cérebro.
Atualmente, as redes neurais são usadas amplamente em muitas tarefas de reconhecimento, classificação, memória associativa, determinando padrões, prevendo etc.
Ao fim de trabalhar com redes neurais existem produtos matemáticos separados e módulos adicionais para os principais pacotes de software matemáticos que fornecem amplas capacidades de construção de redes de diferentes tipos e configurações.
Nós, por outro lado, tentamos criar nossa própria rede neural a partir do zero, por meio da NTL + linguagem e tentar ao mesmo tempo as suas capacidades de programação orientada a objetos.
Escolhendo uma tarefa
Neste artigo, vamos verificar a hipótese de que em base de barras passadas é possível prever com certa probabilidade, o tipo do seguinte barra: subindo ou caindo.
Esta tarefa está relacionada com os de classificação. Temos também uma vasta informação histórica sobre os instrumentos financeiros à nossa disposição, o que permite usar esses dados históricos para obter (especialista) saída desejada. Devido a isso, vamos criar uma rede baseada em percepção multi-camada .
Agora, vamos tentar criar uma rede que prevê, com base em preços de fechamento das k barras, o tipo do seguinte barra. Se o seu preço de fechamento for superior ao preço de fechamento da barra anterior, assumimos a saída desejada para ser 1 (o preço subiu). Em outros casos, vamos supor que a saída desejada é 0 (o preço não mudou ou caiu).
Construindo a rede
Em geral, um percepção multi-camada tem uma camada de entrada, uma ou várias camadas ocultas e uma camada de saída. Tendo uma única camada oculta é suficiente para transformar as entradas de tal forma a dividir linearmente a entrada. Usando mais camadas escondidas, muitas vezes provoca diminuição significativa da velocidade de formação de uma rede sem qualquer vantagem notável na qualidade da aprendizagem.
xVamos resolver em uma rede com uma camada de entrada, uma oculta e uma camada de saída. A figura a seguir mostra a arquitetura de nossa rede em termos gerais.1 - xn - inputs (valores de fechamento), wi,j -pesos das arestas vindo de i-node e vai j-node ;
y1 - ym neurones de camadas escondidas, o1 - ok saidas de network.
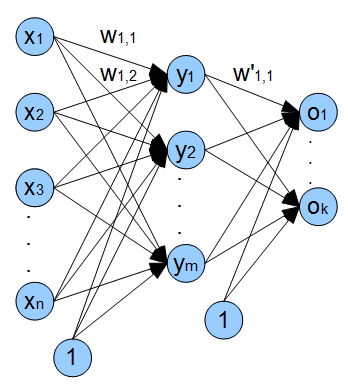
Além disso, há entradas na rede de polarização. Uso desses insumos fornece a capacidade de nossa rede para mudar a função de ativação ao longo do eixo-x, assim, não só a rede mudar a inclinação da função de ativação, mas fornecer seu deslocamento linear.
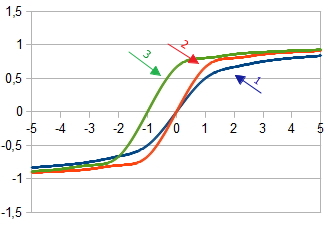
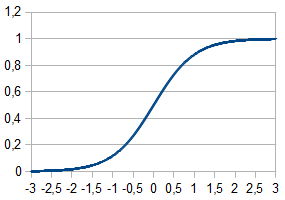
1. Gráfico da função de ativação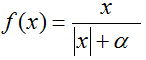 at
at 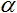 = 1
= 1
2. Gráfico da função de ativação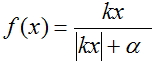 at
at 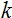 =2 and
=2 and 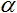 = 1
= 1
3. Gráfico da função de ativação com a mudança 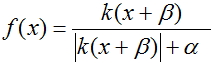 at
at 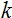 =2,
=2, 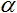 = 1 and
= 1 and 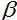 = 1
= 1
O valor para cada nó da rede será calculado de acordo com a fórmula:
o número de nódulos na camada anterior.
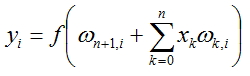 , onde f(x) - função de ativação en
, onde f(x) - função de ativação en
Funções de ativação
A activação da função calcula o sinal de saída, depois de passar recebida do acumulador. Neurónio artificial é geralmente representada como uma função não-linear de um único argumento. Na maioria das vezes são utilizadas as seguintes funções de ativação.
Função Fermi (sigmóide exponencial):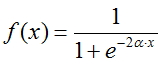
Sigmóide Racional:
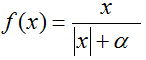
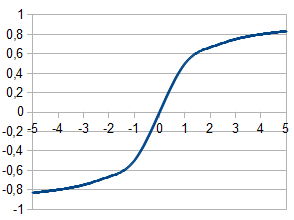
Tangente Hiperbólica:
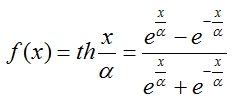
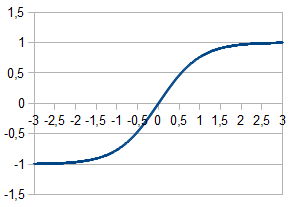
A fim de calcular as saídas de cada camada, sigmóide racional foi escolhido porque o seu cálculo leva menos tempo do processador.
Processo de treinamento da rede
Para treinar a nossa rede, vamos implementar o método de propagação de volta. Este método é um algoritmo iterativo que é usado para minimizar o erro de trabalho de um perceptron multi-camada. A ideia fundamental do algoritmo: depois de calcular os resultados da rede, os ajustamentos para cada nó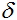 e erro ω para cada aresta são calculadas, pelo que o cálculo de erro vai na direção de saídas de rede para suas entradas. Em seguida, a correção dos pesosω ocorre de acordo com os valores de erros calculados. Este algoritmo impõe a única exigência sobre a função de ativação - deve ser diferenciada. Sigmoids e tangente hiperbólica cumprem este requisito.
e erro ω para cada aresta são calculadas, pelo que o cálculo de erro vai na direção de saídas de rede para suas entradas. Em seguida, a correção dos pesosω ocorre de acordo com os valores de erros calculados. Este algoritmo impõe a única exigência sobre a função de ativação - deve ser diferenciada. Sigmoids e tangente hiperbólica cumprem este requisito.
Agora, para realizar o processo de formação, temos a seguinte seqüência de passos:
- Inicialize os pesos de todas as arestas com valores aleatórios pequenos
- Calcule ajustes para todas as saídas da rede
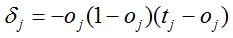 , onde oj - saída calculada da rede, tj - valor esperado (factual)
, onde oj - saída calculada da rede, tj - valor esperado (factual) - Para cada nó, exceto para a última calculamos o ajuste de acordo com a fórmula
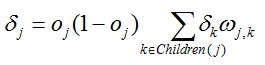 , onde ωj,k
pesos nas extremidades provenientes do nó para o qual é calculado o ajuste e
, onde ωj,k
pesos nas extremidades provenientes do nó para o qual é calculado o ajuste e 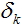 ajustamentos calculados para os nodos situados mais perto da camada de saída.
ajustamentos calculados para os nodos situados mais perto da camada de saída.
- Calcule o ajuste para cada extremidade da rede:
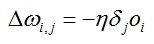 , onde oi saída calculada do nó a partir do qual a borda vem. O erro é calculado para este ponta e
, onde oi saída calculada do nó a partir do qual a borda vem. O erro é calculado para este ponta e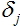 -ajuste calculado para o nó ao qual a borda especificada vem.
-ajuste calculado para o nó ao qual a borda especificada vem. - Valores peso correto para todas as bordas:
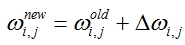
- Repita os passos 2-5 para todos os exemplos de treinamento ou até que o critério conjunto de qualidade de aprendizagem é cumprida
Preparação dos dados de entrada
É necessário preparar os dados de entrada para executar processo de formação da rede, os dados de entrada de alta qualidade tem um impacto significativo sobre o trabalho da rede e a velocidade de estabilização seus coeficientes ω, i.e. no próprio processo de formação.
Todos os vectores de entrada são recomendados para ser normalizados, de modo a que os seus componentes se encontram no intervalo [0, 1] ou [-1, 1]. A normalização faz com que todos os vetores de entrada proporcionam no processo de formação da rede, portanto, procedimento de treinamento correto seja alcançado.
Nós vamos normalizar nossos vetores de entrada - transformar os valores de seus componentes para o intervalo [0, 1], para fazer isso, vamos aplicar a fórmula:
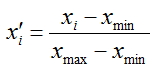
Preços de fechamentos das barras serão utilizados como componentes do vector. Aqueles com índices [n + k, n +1] devem ser alimentados como saídas, onde k - dimensão do vetor de entrada. Iremos determinar o valor desejado com base na barra de ordem n.
Vamos formar o valor em razão da seguinte lógica: se o preço de fechamento para a barra de n-th é superior ao preço de fechamento do n +1 barra (o preço subiu), vamos definir a saída desejada a 1, em caso do preço caiu ou não mudar, vamos definir o valor como 0;
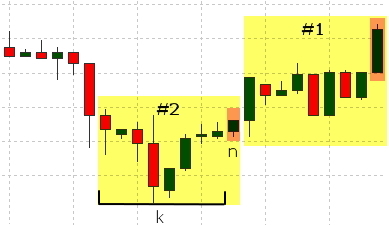
As barras envolvidas na formação de cada conjunto são destacadas em amarelo na figura, a barra que é usado para determinar o valor desejado é realçada em laranja.
A seqüência de dados fornecidos também afeta o processo de formação. O processo de treinamento acontece estável se todos os vetores de entrada correspondem a 1 e 0 são alimentados de maneira uniforme.
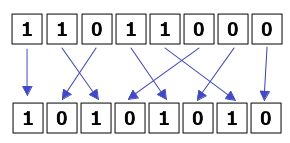
Além disso, vamos formar um conjunto separado de dados que são usados para a avaliação da eficácia de nossa rede. A rede não vai ser treinado sobre esses dados e só serão utilizados para o cálculo do erro com o método dos mínimos quadrados. Nós vamos adicionar 10% dos exemplos iniciais de um conjunto de dados de teste. Como resultado, usaremos 90% dos exemplos para a formação e 10% para o ensaio.
Função, calculando o erro com o método dos mínimos quadrados, fica assim:
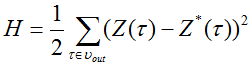 ,
,
onde 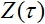 -sinal de saída da rede e
-sinal de saída da rede e 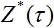 - valor desejado do sinal de saída.
- valor desejado do sinal de saída.
Agora vamos examinar o código de script, preparando-se vetores de entrada para a nossa rede neural.
Vamos considerar classe DataSet - conjunto de dados. A classe inclui:.
- Matriz de vetores de valores de entrada - entrada
- Valor de saída Formado - Saída
- 'Método Normalização '- Normalização dos dados
- Método 'OutputDefine' - determinação do valor real sobre a relação de preços
- Método 'AddData "- valores de gravação na matriz vetor de entrada e variável valor real
- Método 'Arquivização' - a coleta de dados na matriz comum para a gravação posterior no arquivo
Agora vamos examinar o código do programa, usado a função Run () e realizar a seguinte seqüência de ações:
- Carregando todos os dados históricos que está disponível no terminal para uma matriz interior. O carregamento é realizado para o símbolo e os prazos para que o gráfico atual é exibida.
- Corte a matriz bar para o tamanho que é n vezes do vetor de entrada + valor de saída
- Formando as matrizes de vetores de entrada; normalizar estes vectores; determinar o valor desejado 0 ou 1
- Formando a matriz de vectores de entrada, onde os vectores ordenados correspondentes a 0 e um alternativo, sucessivamente
- Gravando a parte principal da matriz com os vectores de entrada ordenados no ficheiro com os dados de gravação e a parte restante dos dados na matriz para o teste e, subsequentemente, com o método de estimativa de mínimos quadrados.
Você também precisa declarar a variável int estado = 0 global neste arquivo, a variável é necessária para a alternância de vetores de entrada.
Criação de classes de rede
Vamos precisar para a nossa rede:
- uma instância da classe "camada" para conexão de entrada e as camadas ocultas da rede
- uma instância da classe "camada" para conectar as camadas ocultas e de saída da rede
- uma instância da classe 'net' para as camadas de ligação da nossa rede
Criando a classe "camada"
Agora, vamos precisar da classe, contendo as seguintes propriedades e métodos:
- array 'input'para armazenar as entradas da rede
- array 'output'para armazenar as saídas da rede
- array 'delta' para armazenar ajustes
- array dois dimensionais 'weights' for edges' weights
- Metodo 'LoadInputs' para atribuir os valores especificados na matriz de entrada de insumos da camada
- Metodo 'LoadWeights'para carregar os valores de peso da camada do disco rígido
- Metodo 'SaveWeights' para salvar os valores de peso da camada para o disco rígido
- construtor aloca o volume de memória necessária para as matrizes utilizadas
- Metodo 'RandomizeWeights' - preenchendo os pesos com valores aleatórios
- Metodo 'OutputCalculation' -calcula os valores de saída
- Metodo 'CalculatingDeltaLast' e 'CalculatingDeltaPrevious' - calcula os valores de saída
- Metodo 'WeightsCorrection' - corrigindo os valores de peso
- metodo adicional de diagnostico (diagnostico) métodos para exibir informações na tela:
- PrintInputs() - imprimir as entradas de uma camada
- PrintOutputs() - imprimindo a saída de uma camada (é chamado após o cálculo de saída por meio de 'OutputCalculation')
- PrintDelta() - ajustes de impressão de uma camada (deve ser chamado depois de calcular os ajustes por meio de 'CalculatingDeltaLast' ou 'CalculatingDeltaPrevious')
- PrintWeights() - impressão de pesos ω da camada
- Metodo 'Calculador' - ligação de nossas camadas para o cálculo da saída de rede. Este método será utilizado mais tarde para o trabalho com a rede treinada
- Metodo 'Calcule e Aprenda ' -saídas de computação, ajustes e erros. Vamos chamar o método anterior para calcular as saídas, e para ajustes e erros que irá chamar os métodos correspondentes de cada camada
- Metodo 'SaveNetwork' -Economizando coeficientes (pesos) da rede .
- Method 'LoadNetwork' - Coeficientes de carga (pesos) da rede.
- cria objeto NT da classe 'net'
- lê coeficientes (pesos) ω e possivel abri-los em NT
- cria matrizes de entradas e saídas da rede
- lê entradas em um loop e coloca-los em 'x' array, lê saídas e coloca-los em ordem de 'reais'
- calcula a saída da rede, alimentando matriz 'x', como uma entrada
- avalia errorcomo a soma dos quadrados das diferenças entre todos os valores calculados e os valores esperados (de facto)
- quando o fim do arquivo é alcançado, exibimos o erro e terminar o trabalho do roteiro
Vamos remover a classe criada para um arquivo separado. Além disso, este arquivo conterá também a configuração de rede: número de nós de entrada, escondida e camadas de saída. Estas variáveis foram colocados fora da classe, a fim de que possam ser utilizadas no script para a preparação de dados de entrada.
Precisaremos também de funções adicionais que vamos colocar fora das aulas. Estas são duas funções: normalização de um vetor de entrada e função de ativação.
Criando a classe 'net'
Vamos precisar da classe combinando nossas camadas em uma rede conjunta, portanto tal classe deve ter:
Verificamos o trabalho da rede
Nesta subseção, vamos verificar o trabalho de nossa rede em um exemplo elementar que será usado para determinar a exatidão de classificação de vetores de entrada.
Para este fim, irá usar uma rede com duas entradas, dois nós da camada oculta e uma saída. Vamos definir o parâmetro nu para 1. Os dados de entrada será representada como conjuntos alternados com os conteúdos seguintes:
input 1,2 e o valor esperado deve ser 1
input 2,1 e o valor esperado deve ser 0
Eles vão ser especificados no arquivo desta forma:
Alimentando número diferente de conjuntos de treinamento para a entrada, podemos observar como o processo de formação da nossa rede está avançando.
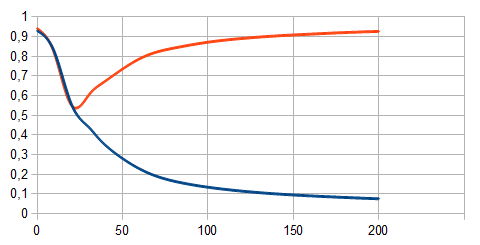
A linha vermelha no gráfico mostra os conjuntos de treinamento correspondentes a 1. A linha azul - corresponde a 0. O número de exemplos de treinamento é demitido ao longo do eixo x, eo valor calculado de rede - ao longo do eixo-y. É óbvio que, quando há alguns barras (25 ou menos) a rede não reconhece diferentes vectores de entrada, quando há mais de um entre eles - a divisão em duas classes é aparente.
Avaliação do funcionamento da rede
Para avaliar a eficácia do treinamento, vamos usar a função de calcular o erro com o método dos mínimos quadrados. Para isso, vamos criar o utilitário com o seguinte código e executá-lo. Vamos precisar de dois arquivos para o seu trabalho: "test.txt" - dados e valores desejados (outputs) que são utilizados na correção de erros e "NT.txt" - o arquivo com os coeficientes calculados (pesos) para o trabalho da rede .
Este script executa a seguinte seqüência de ações:
Criação de um indicador
Vamos criar um indicador que mostra a decisão da rede sobre o próximo bar, por meio de um histograma. A lógica do trabalho do indicador é simples. O valor 0 corresponderá ao valor de queda do próximo bar, valor 1 - aumento do valor, e 0,5 - os eventos de diminuição e aumento de preço de fechamento são igualmente possíveis. Para mostrar o indicador em uma janela separada, vamos especificar
#set_indicator_separate, também é necessário para determinar o arquivo onde a classe 'net' é definido, vamos incluir o arquivo na linha #include "Libraries\NN.ntl". Além disso, vamos precisar de uma variável para armazenar a saída computadorizada de rede para a entrada de dados, se houver apenas um valor de saída, então é suficiente para ter uma variável, mas a rede pode ter várias saídas, portanto, terá um array de valores: nós declará-la na linha de linhs .Na função de inicialização do nosso indicador vamos especificar os parâmetros do indicador, o seu tipo, os valores de vinculação de histograma com dois buffers de valores. Também vai precisar para restaurar parâmetros da nossa rede, ou seja, carga nele todos os coeficientes de peso, calculado durante o processo de treinamento. Isso é feito por meio do método LoadNetwork (string s) de objeto NT, com o único parâmetro - o nome do arquivo que contém os coeficientes de peso. Na função Draw formamos vetor de entrada x correspondendo a preços de fechamento das barras com os índices [pos + inputVectorSize-1; pos], onde 'pos' - número do bar que calculamos o valor e dimensão "inputVectorSize" do vetor de entrada. No final, o método 'Calcular' do objeto NT é chamado. Ele retorna uma matriz de valores (se a nossa rede tem várias saídas), mas porque temos apenas uma saída, vamos usar o elemento do array com índice 0.
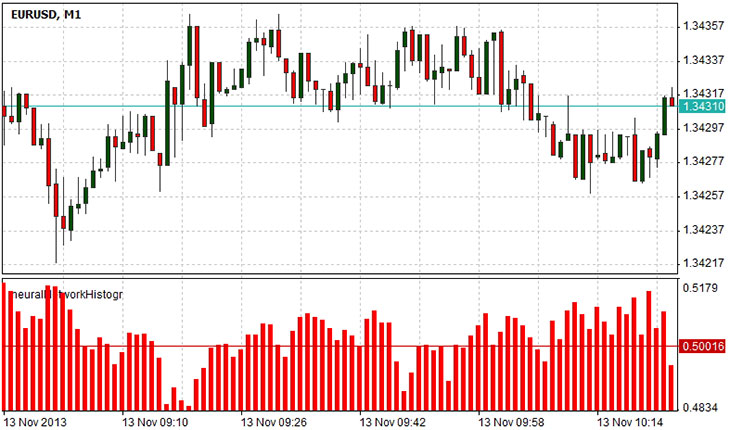
O diagrama acima mostra a previsão da rede da barra subseqüente. Valores 0,5-1 sugerem a maior possibilidade de que barra posterior subirá de queda. Valores 0-0,5 implicam maior possibilidade de cair em vez de subir. Valor 0,5 sugere o estado de ambivalência: o próximo barra pode ir para cima ou para baixo.
Resumo
As redes neurais são ferramentas poderosas para análise de dados. Este artigo abordou o processo de criação de uma rede neural, por meio de programação orientada a objetos no NTL + linguagem. O uso de programação orientada a objetos permitiu simplificar o código e tornou muito mais reutilizável nos scripts futuros. Na implementação apresentado que precisávamos para criar a camada de classe a definição de uma camada da rede neural ea classe net definição da rede em geral. Usamos a classe 'net' para o indicador, o cálculo de erros e cálculo dos pesos internos da rede. Além disso, foi apresentado como usar a rede treinada pelo exemplo do indicador de histograma que, desde a previsão da rede da mudança de preço.
